不正の検出
ベンフォードの法則インジケーター(第1桁の法則)は、数値データの数字1から9の出現率を検証するものです。これはリストやテーブルから会計や経費に関する不正を察知するためのインジケーターとして使用されます。
ベンフォードの法則では、リストやテーブルにおいて、数字1が1桁目に表れる確率は約30%であるとされています。大きい数字が1桁目に表れる頻度は低く、たとえば2という数字は17%、3という数字は12%となっています。有効で改ざんされていないデータであれば、この出現頻度に沿ったものとなるはずです。分析したデータにおける第1桁の頻度分布とベンフォードの法則で予想される分布を比較することで異常な結果を識別できます。
たとえば、従業員が架空の業者を作り出して送金する不正を行ったとします。これら架空の支払の金額は自然に発生したものではなく、作り出されたものなので、架空の取引および正当な取引すべて(両者混合)の第一桁の分布はベンフォードの法則に則したものではなくなります。さらに、これら不正な支払の多くで、第1桁に2があった(29、232、2187など)とします。ベンフォードの法則インジケーターを使用してこのようなデータを分析すると、第1桁に2を持つ金額が、通常の出現パターンである17%よりも頻繁に出現していることが分かります。
ベンフォードの法則インジケーターを使用する時は、分析する数値データが0で始まっていないことを確認します。ベンフォードの法則では第1桁が1から9の範囲であることが期待されています。これは、分析するカラムに[number] (数) > [Integer values] (整数値)パターンを使用することで確認できます。
ベンフォードの法則インジケーターの結果図では、1から9の数字が棒で表されており、棒の高さが分析したデータにおける第1桁の頻度分布をパーセントで表しています。点はベンフォードの法則に従った予想される第1桁の頻度分布を表しています。
以下は、ベンフォードの法則インジケーターを使用した分析の結果と、total_salesカラムにユーザー定義インジケーターのOrder of Magnitude (桁数)を使用した例です。
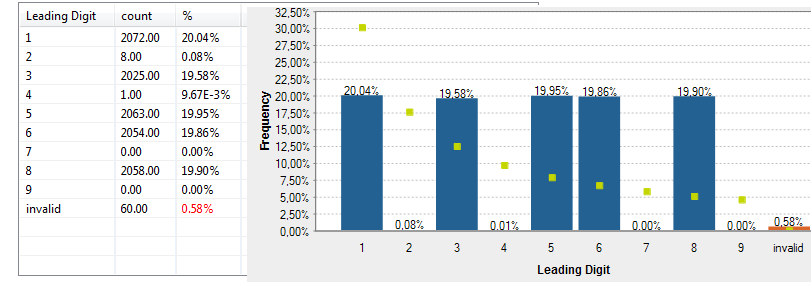
この図は、データの実際の分布(棒の高さ)がベンフォードの法則(点の値)に則していないことを示しています。売上額の頻度分布とベンフォードの法則で予想される分布の間には大きな相違が見られます。たとえば、1で始まる売上額の通常の出現パターンは30%ですが、分析されたデータでは20%しかないことが分かります。不正の可能性が疑われます。何者かによって売上額が変更されたかデータが一部存在しない可能性があります。
以下は、ベンフォードの法則インジケーターを使用したカラム分析結果図の別の例です。
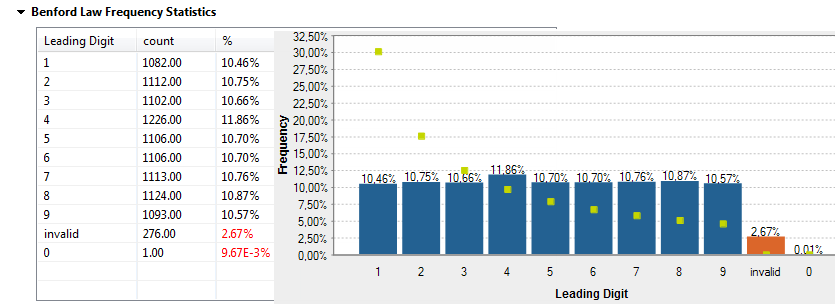
[Invalid] (無効)というラベルの付いた赤い棒は分析されたデータのうち、数字で始まっていないものの割合を表しています。0バーは0で始まるデータの割合を示します。どちらもベンフォードの法則インジケーターを使ったカラム分析では予想されていないものであるため、赤で表されています。
どのデータベースでも選択できるインジケーターを次のテーブルに示します。
| データ型 | 数字 | Text | Date | その他 | ||||
|---|---|---|---|---|---|---|---|---|
| 分析エンジンのタイプ | Java | SQL | Java | SQL | Java | SQL | Java | SQL |
| ベンフォードの法則 |

|

|

|

|

|

|

|

|
